문제 설명
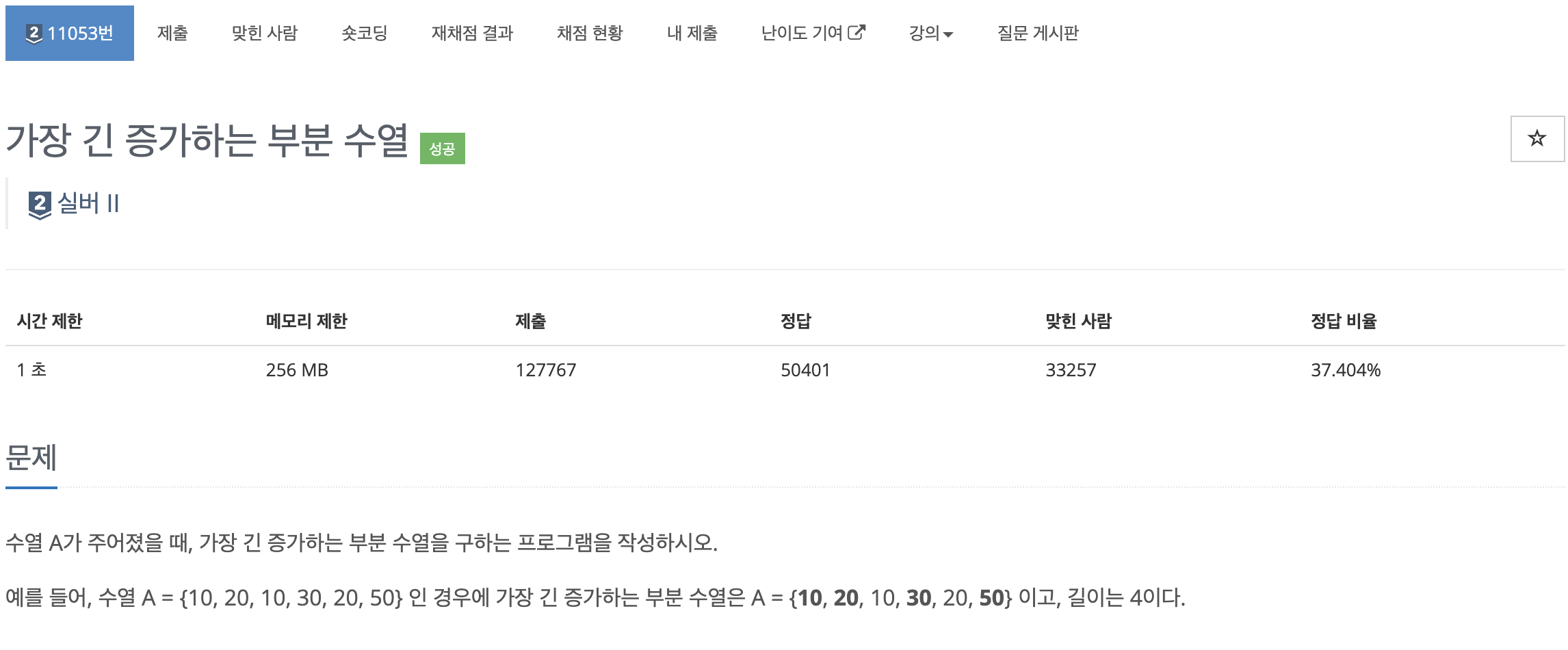
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오.
예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.
입력
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000)이 주어진다.
둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ Ai ≤ 1,000)
출력
첫째 줄에 수열 A의 가장 긴 증가하는 부분 수열의 길이를 출력한다.
문제분석과정
가장 긴 증가하는 부분 수열을 구하기 위해서 어떻게해야할까 ?
일단 메모지에이션을 하기위해 dp를 정의하고 dp[1]뭔지 찾아보자
dp를 어떻게 정의해야할지 감이 오지않으니까 증가부분수열을 관찰해보자
i에 대한 분석
6
10 20 10 30 20 50 이 주어졌을 때,
10 - 1 /
10 20 - 2 /
10 20 10 - 1 /
10 20 10 30 - 3 /
10 20 10 30 20 - 2 /
10 20 10 30 20 50 - 4 /dp[끝나는 인덱스] = 끝나는 인덱스 일때 최장 부분 수열
한칸씩 이동하며 전체적으로 증가시킴
모든 초기값은 자기자신 한 개인 경우로 1개이다.
10 20 10 30 20 50 일 때
1 1 1 1 1 1 1 / i = 2
1 1 2 1 1 1 1 / i = 3
1 1 2 1 3 1 1 / i = 4
1 1 2 2 3 2 1 / i = 5
1 1 2 2 3 2 4 / i = 6j에 대한 분석
점화식 을 찾기 위해서 i = 5를 관찰해보자, 20과 같거나 큰 녀석들은 무시한다.
1 1 2 1 3 1 1 / 현재 dp Table
10 10 20(현재 피벗) dp[4] = 1
1 1 2 1 3 1 1 / 현재 dp Table / j = 1
10(체크)10 20(현재 피벗) dp[4] = (1 , dp[1]+1 = 2)
1 1 2 1 3 1 1 / 현재 dp Table / j = 4
10 10(체크)20(현재 피벗) dp[4] = max(1 , dp[4]+1 = 2)i를 조사할때, 현재까지 인덱스i로 끝나는 녀석
인덱스j로 조사하는데 인덱스j로 끝나는 녀석에게 인덱스i를 붙힌 녀석
둘중 큰값을 dp[i]로 최신화 되며, j를 다돌면 dp[i]가 산정된다.
각 i 마다 위과정들을 다 거친후 max(dp) 하게되면 정답을 구할 수 있다.
한 가지 주의 사항은 0번째 index를 추가해줄때 입력값을 고려해서 추가해줘야한다.
입력으로 1000 보다 큰 수가 나올 수 없으므로 정답에 영향을 주지 못한다.
다른 방법으로는 dp ,arr 의 크기를 n+1 이아니라 n으로 초기화해도 가능하지만 다이나믹 프로그래밍 알고리즘은 리스트의 인덱스를 헷갈리지않게 처리해야하므로 입력값을 고려하는게 더 좋은 선택이라고 생각한다.
n = int(input())
arr = [1001] + list(map(int,input().split()))
# 가장 긴 증가하는 부분 수열을 구하기 위해서 어떻게해야할까 ?
# 일단 메모지에이션을 하기위해 dp를 정의하고 dp[1]뭔지 찾아보자
# dp를 어떻게 정의해야할지 감이 오지않으니까 증가부분수열을 관찰해보자
# 10 - 1
# 10 20 - 2
# 10 20 10 - 1
# 10 20 10 30 - 3
# 10 20 10 30 20 - 2
# 10 20 10 30 20 50 - 4
# dp[끝나는 인덱스] = 끝나는 인덱스 일때 최장 부분 수열
# 한칸씩 이동하며 전체적으로 증가시킴
# 모든 초기값은 자기자신 한 개인 경우로 1개이다.
# 10 20 10 30 20 50 일 때
#1 1 1 1 1 1 1 / i = 2
#1 1 2 1 1 1 1 / i = 3
#1 1 2 1 3 1 1 / i = 4
#1 1 2 2 3 2 1 / i = 5
#1 1 2 2 3 2 4 / i = 6
# 점화식 을 찾기 위해서 i = 5를 관찰해보자
# 20과 같거나 큰 녀석들은 무시한다.
# 1 1 2 1 3 1 1 / 현재 dp Table
# 10 10 20(현재 피벗) dp[4] = 1
# 1 1 2 1 3 1 1 / 현재 dp Table / j = 1
# 10(체크)10 20(현재 피벗) dp[4] = (1 , dp[1]+1 = 2)
# 1 1 2 1 3 1 1 / 현재 dp Table / j = 4
# 10 10(체크)20(현재 피벗) dp[4] = max(1 , dp[4]+1 = 2)
# i를 조사할때
# 현재까지 인덱스i로 끝나는 녀석
# 인덱스j로 조사하는데 인덱스j로 끝나는 녀석에게 인덱스i를 붙힌 녀석
# 둘중 큰값을 dp[i]로 최신화. j를 다돌면 dp[i]가 산정된다.
# 위과정들을 다
# 정답은 max(dp)
dp = [1]*(n+1)
for i in range(2,n+1):
for j in range(1,i):
if arr[i] > arr[j]:
dp[i] = max(dp[i], dp[j] + 1)
print(max(dp))분류
다이나믹 프로그래밍(dp)
'PS > DP' 카테고리의 다른 글
| [PS][BOJ/11054]-가장 긴 바이토닉 부분 수열 (0) | 2023.02.17 |
|---|---|
| [PS][BOJ/2565]- 전깃줄 (0) | 2023.02.16 |
| [PS][BOJ/10844번] 쉬운 계단수 (0) | 2023.02.14 |
| [PS][BOJ/1912번]-연속합 (0) | 2023.02.13 |
| [PS][BOJ/13699번]-점화식 (0) | 2023.02.10 |

문제 설명
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오.
예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.
입력
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000)이 주어진다.
둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ Ai ≤ 1,000)
출력
첫째 줄에 수열 A의 가장 긴 증가하는 부분 수열의 길이를 출력한다.
문제분석과정
가장 긴 증가하는 부분 수열을 구하기 위해서 어떻게해야할까 ?
일단 메모지에이션을 하기위해 dp를 정의하고 dp[1]뭔지 찾아보자
dp를 어떻게 정의해야할지 감이 오지않으니까 증가부분수열을 관찰해보자
i에 대한 분석
6
10 20 10 30 20 50 이 주어졌을 때,
10 - 1 /
10 20 - 2 /
10 20 10 - 1 /
10 20 10 30 - 3 /
10 20 10 30 20 - 2 /
10 20 10 30 20 50 - 4 /dp[끝나는 인덱스] = 끝나는 인덱스 일때 최장 부분 수열
한칸씩 이동하며 전체적으로 증가시킴
모든 초기값은 자기자신 한 개인 경우로 1개이다.
10 20 10 30 20 50 일 때
1 1 1 1 1 1 1 / i = 2
1 1 2 1 1 1 1 / i = 3
1 1 2 1 3 1 1 / i = 4
1 1 2 2 3 2 1 / i = 5
1 1 2 2 3 2 4 / i = 6j에 대한 분석
점화식 을 찾기 위해서 i = 5를 관찰해보자, 20과 같거나 큰 녀석들은 무시한다.
1 1 2 1 3 1 1 / 현재 dp Table
10 10 20(현재 피벗) dp[4] = 1
1 1 2 1 3 1 1 / 현재 dp Table / j = 1
10(체크)10 20(현재 피벗) dp[4] = (1 , dp[1]+1 = 2)
1 1 2 1 3 1 1 / 현재 dp Table / j = 4
10 10(체크)20(현재 피벗) dp[4] = max(1 , dp[4]+1 = 2)i를 조사할때, 현재까지 인덱스i로 끝나는 녀석
인덱스j로 조사하는데 인덱스j로 끝나는 녀석에게 인덱스i를 붙힌 녀석
둘중 큰값을 dp[i]로 최신화 되며, j를 다돌면 dp[i]가 산정된다.
각 i 마다 위과정들을 다 거친후 max(dp) 하게되면 정답을 구할 수 있다.
한 가지 주의 사항은 0번째 index를 추가해줄때 입력값을 고려해서 추가해줘야한다.
입력으로 1000 보다 큰 수가 나올 수 없으므로 정답에 영향을 주지 못한다.
다른 방법으로는 dp ,arr 의 크기를 n+1 이아니라 n으로 초기화해도 가능하지만 다이나믹 프로그래밍 알고리즘은 리스트의 인덱스를 헷갈리지않게 처리해야하므로 입력값을 고려하는게 더 좋은 선택이라고 생각한다.
n = int(input())
arr = [1001] + list(map(int,input().split()))
# 가장 긴 증가하는 부분 수열을 구하기 위해서 어떻게해야할까 ?
# 일단 메모지에이션을 하기위해 dp를 정의하고 dp[1]뭔지 찾아보자
# dp를 어떻게 정의해야할지 감이 오지않으니까 증가부분수열을 관찰해보자
# 10 - 1
# 10 20 - 2
# 10 20 10 - 1
# 10 20 10 30 - 3
# 10 20 10 30 20 - 2
# 10 20 10 30 20 50 - 4
# dp[끝나는 인덱스] = 끝나는 인덱스 일때 최장 부분 수열
# 한칸씩 이동하며 전체적으로 증가시킴
# 모든 초기값은 자기자신 한 개인 경우로 1개이다.
# 10 20 10 30 20 50 일 때
#1 1 1 1 1 1 1 / i = 2
#1 1 2 1 1 1 1 / i = 3
#1 1 2 1 3 1 1 / i = 4
#1 1 2 2 3 2 1 / i = 5
#1 1 2 2 3 2 4 / i = 6
# 점화식 을 찾기 위해서 i = 5를 관찰해보자
# 20과 같거나 큰 녀석들은 무시한다.
# 1 1 2 1 3 1 1 / 현재 dp Table
# 10 10 20(현재 피벗) dp[4] = 1
# 1 1 2 1 3 1 1 / 현재 dp Table / j = 1
# 10(체크)10 20(현재 피벗) dp[4] = (1 , dp[1]+1 = 2)
# 1 1 2 1 3 1 1 / 현재 dp Table / j = 4
# 10 10(체크)20(현재 피벗) dp[4] = max(1 , dp[4]+1 = 2)
# i를 조사할때
# 현재까지 인덱스i로 끝나는 녀석
# 인덱스j로 조사하는데 인덱스j로 끝나는 녀석에게 인덱스i를 붙힌 녀석
# 둘중 큰값을 dp[i]로 최신화. j를 다돌면 dp[i]가 산정된다.
# 위과정들을 다
# 정답은 max(dp)
dp = [1]*(n+1)
for i in range(2,n+1):
for j in range(1,i):
if arr[i] > arr[j]:
dp[i] = max(dp[i], dp[j] + 1)
print(max(dp))분류
다이나믹 프로그래밍(dp)
'PS > DP' 카테고리의 다른 글
| [PS][BOJ/11054]-가장 긴 바이토닉 부분 수열 (0) | 2023.02.17 |
|---|---|
| [PS][BOJ/2565]- 전깃줄 (0) | 2023.02.16 |
| [PS][BOJ/10844번] 쉬운 계단수 (0) | 2023.02.14 |
| [PS][BOJ/1912번]-연속합 (0) | 2023.02.13 |
| [PS][BOJ/13699번]-점화식 (0) | 2023.02.10 |
