문제 설명
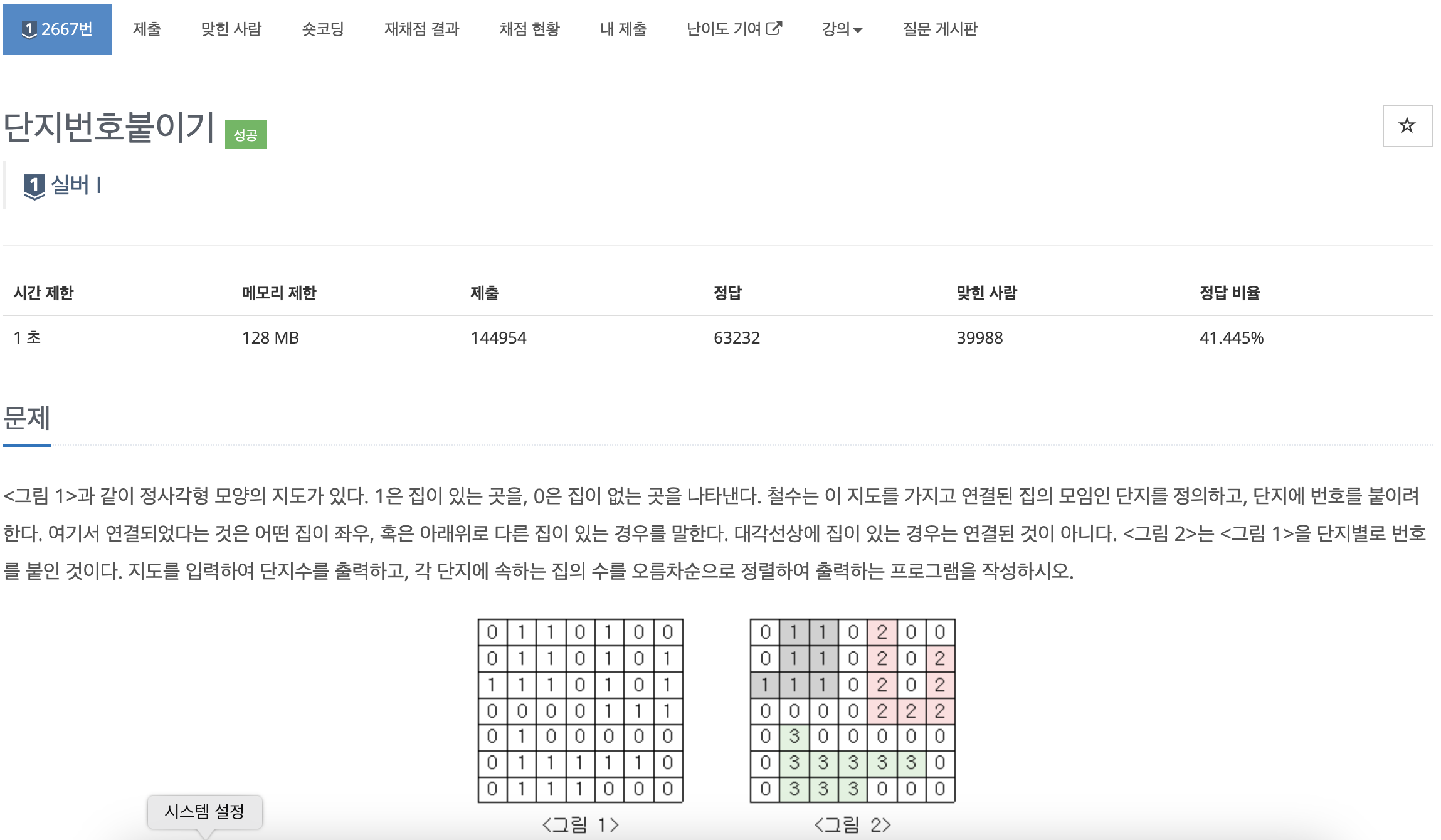
<그림 1>과 같이 정사각형 모양의 지도가 있다. 1은 집이 있는 곳을, 0은 집이 없는 곳을 나타낸다. 철수는 이 지도를 가지고 연결된 집의 모임인 단지를 정의하고, 단지에 번호를 붙이려 한다. 여기서 연결되었다는 것은 어떤 집이 좌우, 혹은 아래위로 다른 집이 있는 경우를 말한다. 대각선상에 집이 있는 경우는 연결된 것이 아니다. <그림 2>는 <그림 1>을 단지별로 번호를 붙인 것이다. 지도를 입력하여 단지수를 출력하고, 각 단지에 속하는 집의 수를 오름차순으로 정렬하여 출력하는 프로그램을 작성하시오.

입력
첫 번째 줄에는 지도의 크기 N(정사각형이므로 가로와 세로의 크기는 같으며 5≤N≤25)이 입력되고, 그 다음 N줄에는 각각 N개의 자료(0혹은 1)가 입력된다.
출력
첫 번째 줄에는 총 단지수를 출력하시오. 그리고 각 단지내 집의 수를 오름차순으로 정렬하여 한 줄에 하나씩 출력하시오.
문제 분석과정
일단 이 문제는 깊이 우선 탐색을 하는것이 효율적으로 보인다.
딱히 weight 가 있는 것도 아니고 연결된 노드들을 2차원을 탐색하며 판단해야하는 문제이기 때문이다.
이런 경우 DFS 탐색을 활용하는 것이 편하다.
Linked 인 것들을 카운팅하며 연결된 모든 것을 카운팅한다.
방문시 방문했다고 표식을 남기고 표식된 인덱스는 방문 하지않는다.
범위는 기본적인 것이므로 딱히, 이야기는 하지않겠다.
뭐 이런경우 전체탐색하는 것만으로도, 시간복잡도가 O(n^2) 이 되긴 하지만 실제로 큰 문제가 되지는 않는다.
왜냐하면, 2 중 for 문으로 탐색할 때 연결이되는지(범위,방문여부,방문할수있는지)를 확인하므로 거의다 나가리된다.
이렇게 한 섹터의 깊이 우선탐색을 마치면 한 링크된 노드들의 갯수를 알 수 있다.
그 후 2중 for 문으로 연결이되는지를 조사한후 가능한곳을 다시 깊이우선 탐색하게된다.
그럼 이 섹터는 이전 섹터와 구분되는 섹터가되며 섹터를 구성하는 노드를 또 구할 수 있고 그 노드갯수를 결과리스트에 저장한후 오름차순으로 정렬한후 출력하면 정답이 된다.
소스코드
import sys
input = sys.stdin.readline
n = int(input())
# 입력받기
g = [0]*(n+1)
g[0] = [0 for _ in range(n+1)]
for i in range(1,n+1):
g[i] = [0]+list(map(int,input().rstrip()))
# 방문여부 확인을 위한.
visit = [[0 for _ in range(n+1)]for _ in range(n+1)]
# 결과 값을 위한 저장소
totalSection = 0
section = []
global cnt
cnt = 0
# 범위 확인을 위한.
def inRange(x,y):
return 0<x and x<=n and \
0<y and y<=n
# 연결이되었는지 확인을 위한
def isLinked(x,y):
# 범위안이며, 방문한적없고, 유의미한 값이라면 -> 연결된 것으로 간주한다.
return inRange(x,y)and not visit[x][y] and g[x][y]
# 이동을 위한
dxSet = [0,1,0,-1]
dySet = [1,0,-1,0]
#깊이 우선 탐색
def run(px,py):
global cnt
# 현재
visit[px][py] = 1
cnt += 1
for dx,dy in zip(dxSet,dySet):
nx,ny = px+dx,py+dy
if isLinked(nx,ny):
run(nx,ny)
# 모든 경우를 탐색함
for i in range(1,n+1):
for j in range(1,n+1):
cnt = 0
if isLinked(i,j):
totalSection += 1
run(i,j)
section.append(cnt)
print(totalSection)
section.sort()
for secNum in section:
print(secNum)분류
너비 우선 탐색(bfs), 깊이 우선 탐색(dfs), 그래프 이론(graphs), 그래프 탐색(graph_traversal)
